Hacim:Maddenin boşlukta kapladığı uzay parçasıdır.Katı maddelerin hacmini bulmak için katının şekline göre (geometrik ise) Matematiksel formüller kullanırız.Küp için Hacim= V=4/3pr3 Silindir İçin V=pr2h kullanıldığını aklımızda tutmalıyız.zaten dörgen prizma ise üç boyutunu çarpacağız çünkü hacim üç boyutlu bir uzay parçasıdır. Eğer şeklimiz düzgün (Geometrik) değilse o zaman bir dereceli kabın içindeki sıvıya atarak sıvı seviyesinde yaptığı değişime göre hacmini bulabiliriz.Şimdi bunlara örnekler vererek açmaya çalışalım.

Örnek:Şekildeki kürenin, silindirin,dikdörtgenin ve küpün hacimlerini bulalım.

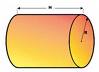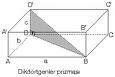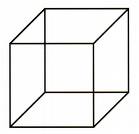
   r=2 cm.                       r=5 m. ve h=10m.    a=5 dm,b=40 cm,c=1mm         a=10 cm.

Çözüm:Küreden başlayalım V=4/3pr3 =4/3.3.2.2.2=32 cm3 olur (cm Cinsinden verilmiş çünkü ) 

Silindir: V=pr2h=3.5.5.10=750 m3 burda da metre cinsinden verilmiş ti.

Dikdörtgen prizma:Hepsini tek birim yapalım çünkü farklı.Ben desimetre seçeyim. V=a.b.c=5.4.100=2000 dm3 olur.

Küpte zaten her kenar eşit V=a3=10.10.10 =1000 cm3

*****Birim çevirmelerinde sıkıntı çekiyorsanız mutlaka birim çalışın derim. Çünkü Yanlış birim kullanmak bir çocuğun manavdan 2 metre domates almasına benzer. Gerçi çocuk bile domatesi aldığına göre Kilo olduğunu bilir.Birimler çin ilk ünite olan fiziğin doğası ünitesine bakınız.daha geniş bilgi için http://www.birimcevir.com/ adresini tıklayınız CTRL ye basılı tıklayınkiz sayanız açık kalsın.

Birde sıvı için örnek yapalım.ne dersiniz?

Çözüm:Eğer kum içinde boşluk olmasaydı toplam hacim 20+10= 30 olacaktı.Azalan su boşlukları doldurduğuna göre boşluk hacmi 30-26=4 ml.=4 cm3 demektir değil mi? Yani 4/10 ü boşluktur. oda 40/100 e eşit olduğundan Kumda  ‰ 40 boşluk var demektir.Kumun net hacmi 10-4=6ml. dir.

 

Kütle,Maddenin Eylemsizlik miktarıdır. Yani diğer maddelere göre ne kadar eylemsizliğe sahip olduğunu ifade eder kütle kavramı. Eşit Kollu terazi ile ölçülür.Çünkü ağırlık gibi yerçekimine bağlı olmayıp bir başka cismin (Standart Kütleler gibi) eylemsizliği ile kıyaslanıp ölçülür.m harfi ile gösterilir ve birimi için Kg ve gr kullanılır.

 

Özkütle.birim hacimdeki madde miktarıdır.Maddenin Kütlesi hacmine bölünerek bulunur.yani maddenin numunesidir.Örneğin zeytin yağının öz kütlesini merak eden bir öğrenci 500 ml pet şişeye zeytin yağı doldurarak kütlesini bulursa onun özkütlesi bulunan kütle/500 olur.Bu da bir Mililitresinin kütlesi demektir.

Karışımların özkütlesi bulunurken karışıma giren tüm maddelerin kütleleri toplamının tüm hacimlerine bölümü yapılır.Yani €m/€V

*özel Olarak karışım eşit hacimdeyse aritmetik ortalama eşit kütlede ise geometrik ortalama ile karışım özkütlesi bulunmalıdır. Bura da grafikler çok önemli arkadaşlar. Yani kütle hacim grafiğinden özkütle bulma işinden bahsediyorum.Normal sorulardan daha kolaydırlar. Şimdi örneklerle karışımların özkütlelerini bulalım.

 

   İlgili Video için Tıklayınız 

 

Örnek:Şekil 1 de x ve y eşit hacimde şekil 2 de ise eşit kütlede karıştırılırsa karışımın özkütleleri ne olur.

           

                                             Şekil-1                                              Şekil-2

Çözüm: Grafiklerin dikey (Y) Sütünü kütle Yatay ise (x) Hacim olarak verilmiş ilk olarak birinci şekil için özkütleleri bulalım.bunun için grafiğin kesişm noktalarına bakacağız.

x için kesişme noktasına bakın dikeyde 40 olduğu yerde kesişmiş. Özkütle =d=m/V=30/40=3/4 ve Y için d=10/40 =1/4 aritmetik ortalama tıpkı not ortalaması gibidir.Yani ikisini topla ikiye böl üç olsa üçünü toplayıp üçe bölecektik.3/4+1/4=4/4=1 onu da ikiye bölersek Karışım için d=1/2 olur.

Şekil 2 de özkütller X-d=20/10=2 Y-d=10/10=1 dir.geometrik ortalama formülü d= 2.dx.dy/(dx+dy) dir.

yerine yazalım.d=2.2.1/(2+1)=4/3 bulunur. 

  

Ağırlık ise kütleye uygulanan yer çekim kuvvetidir.ve kütle çekim sabiti (g) ile çarpılarak bulunur.

Ağırlık=G=m.g dir  

 

 Yer çekim sabiti 9,81 olup genelde yaklaşık olduğu için 10 alınır .Mesela 20 Kilogram kütleli bir cismin ağırlığı  G=m.g den 20.10=200 N dir. Burada N- Newtondur ve ağırlık birimidir.